「堆」

概述

在计算机的世界里，很多的应用场景只需要取得当前数据集中最大或者最小的元素，而对于数据集中其它数据，并不需要他们一定是有序的。那么，我们如何高效快速地取得当前数据集中最大或者最小的元素呢？此时，新的数据结构「堆」就诞生了。 我们将介绍「堆」，完成后，你将： 理解「堆」数据结构和实现； 理解「最大堆」和「最小堆」的基础概念和核心操作； 理解「堆排序」； 理解「堆」的应用场景； 能够运用「堆」解决实际问题。  

堆的定义与分类

堆的定义：根据 维基百科 的定义，堆 是一种特别的二叉树，满足以下条件的二叉树，可以称之为 堆：

1. 完全二叉树；
2. 每一个节点的值都必须 大于等于或者小于等于 其孩子节点的值。

堆 具有以下的特点：

1. 可以在O(logN) 的时间复杂度内向 堆 中插入元素；
2. 可以在O(logN) 的时间复杂度内向 堆 中删除元素；
3. 可以在O(1) 的时间复杂度内获取 堆 中的最大值或最小值。

堆的分类

堆有两种类型：最大堆 和 最小堆。 最大堆：堆中每一个节点的值 都大于等于 其孩子节点的值。所以最大堆的特性是 堆顶元素（根节点）是堆中的最大值。 最小堆：堆中每一个节点的值 都小于等于 其孩子节点的值。所以最小堆的特性是 堆顶元素（根节点）是堆中的最小值。

• 「最大堆」的实现

• 「最小堆」的实现    

扩展延伸：完全二叉树与数组的转换

请判断下图的树是否为堆？

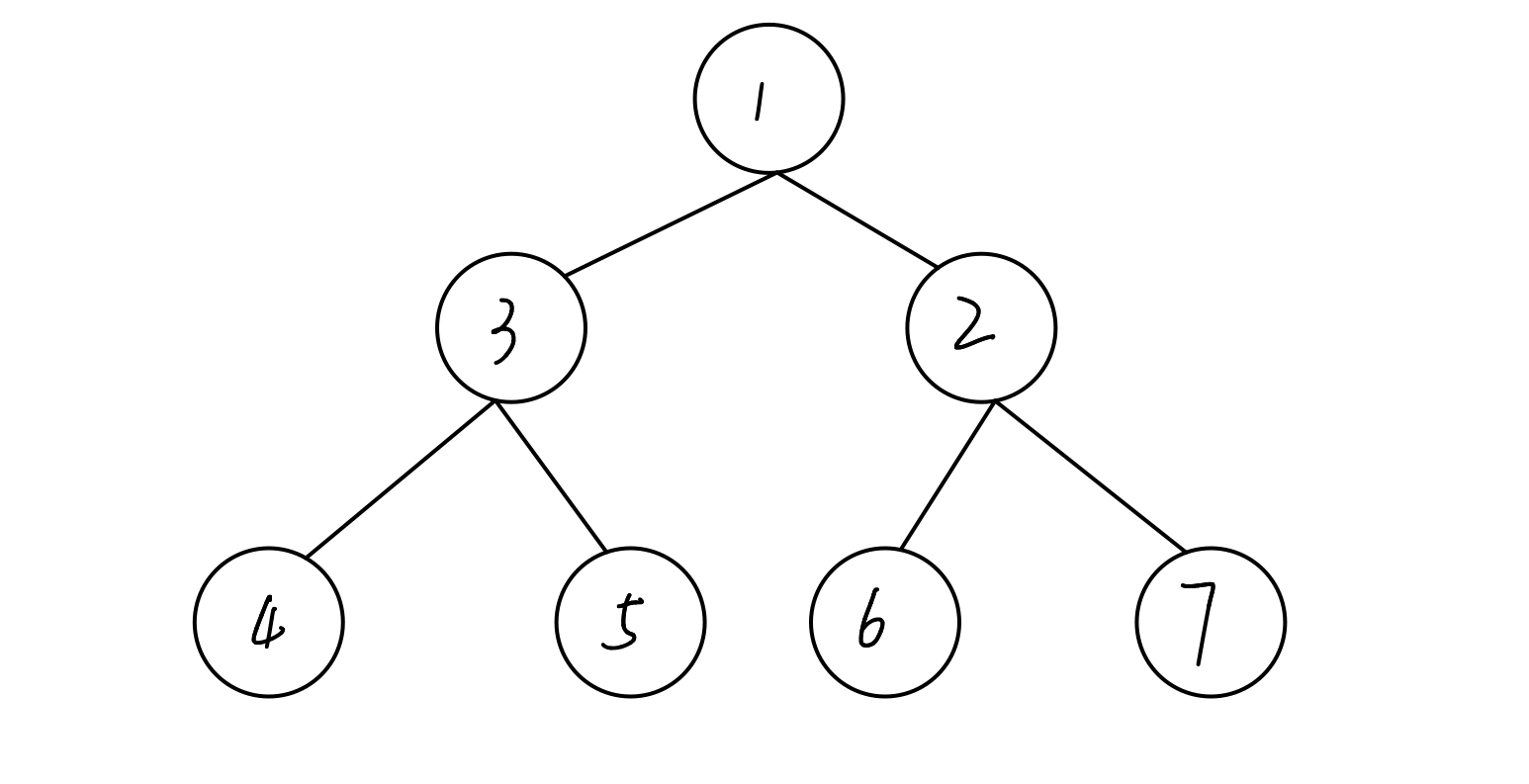
答案：是

解析：这是一个完全二叉树，并且所有节点的值都小于等于其孩子节点。

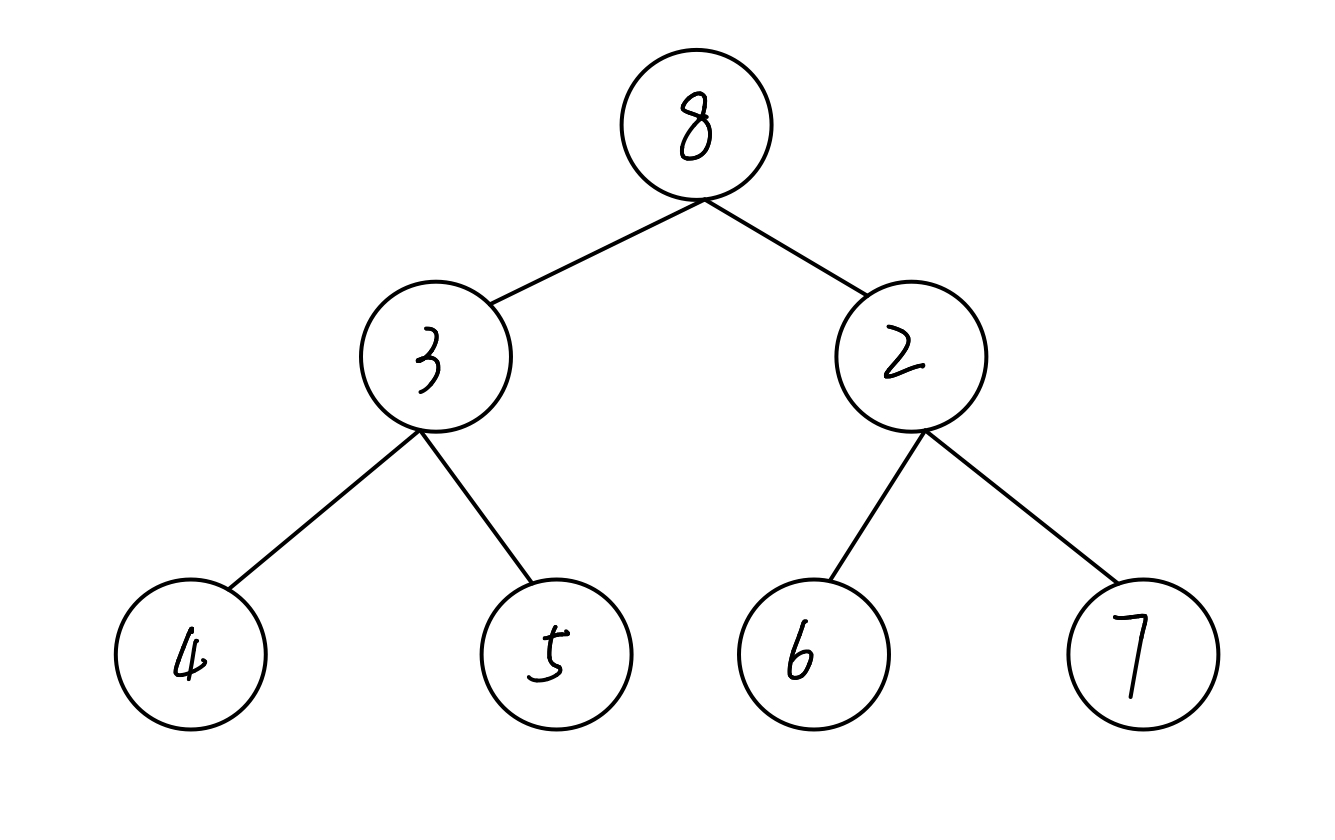
答案：否

解析：这虽然是一个完全二叉树，但是并非所有节点的值都小于等于（或者都大于等于）孩子节点。 第一行的节点比孩子节点大，但第二行的左右节点都比孩子节点小。

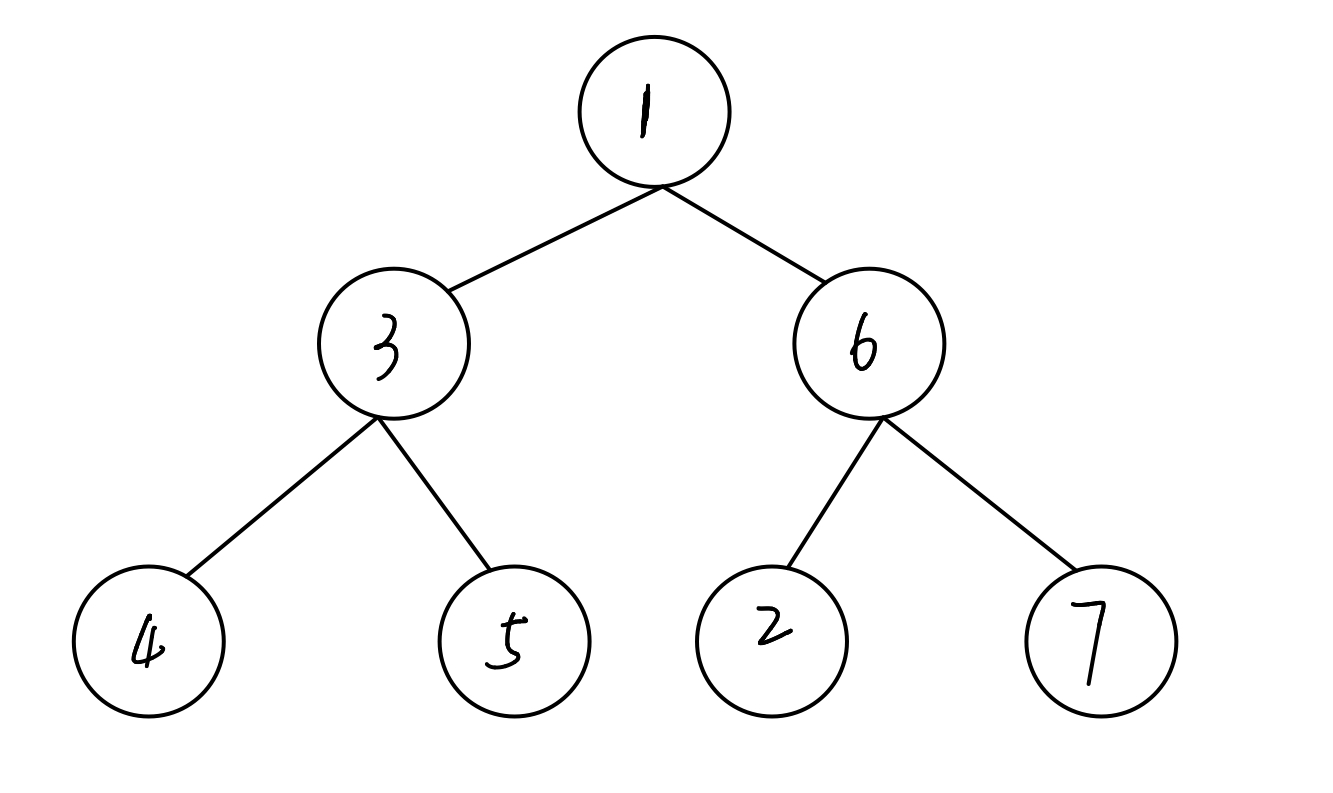
答案：否

解析：这虽然是一个完全二叉树，但是并非所有节点的值都小于等于（或者都大于等于）孩子节点。 第二行的右节点比其左孩子节点的值大。

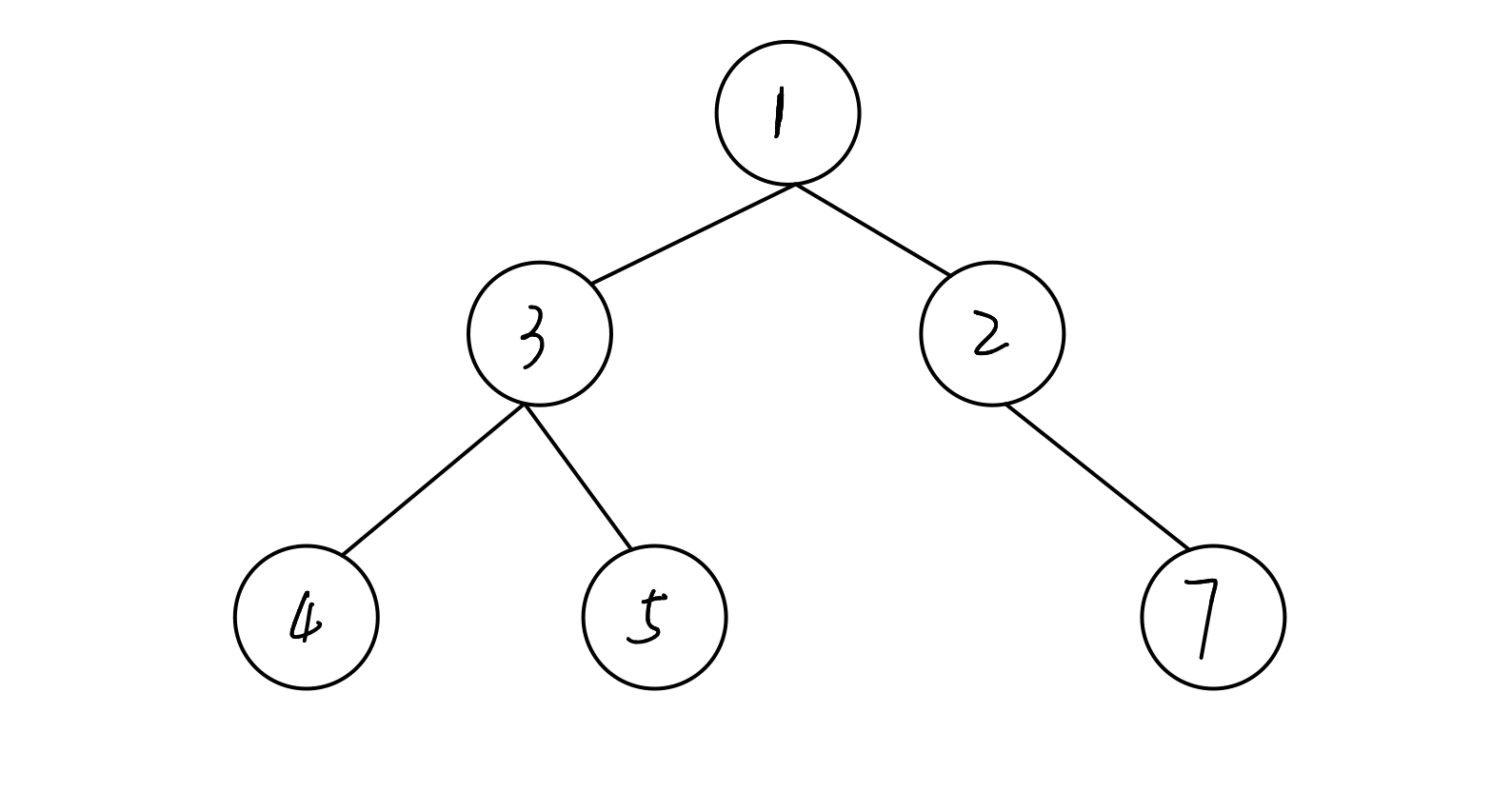
答案：否

解析：虽然所有节点都比孩子节点的值小，但它不是一个完全二叉树。

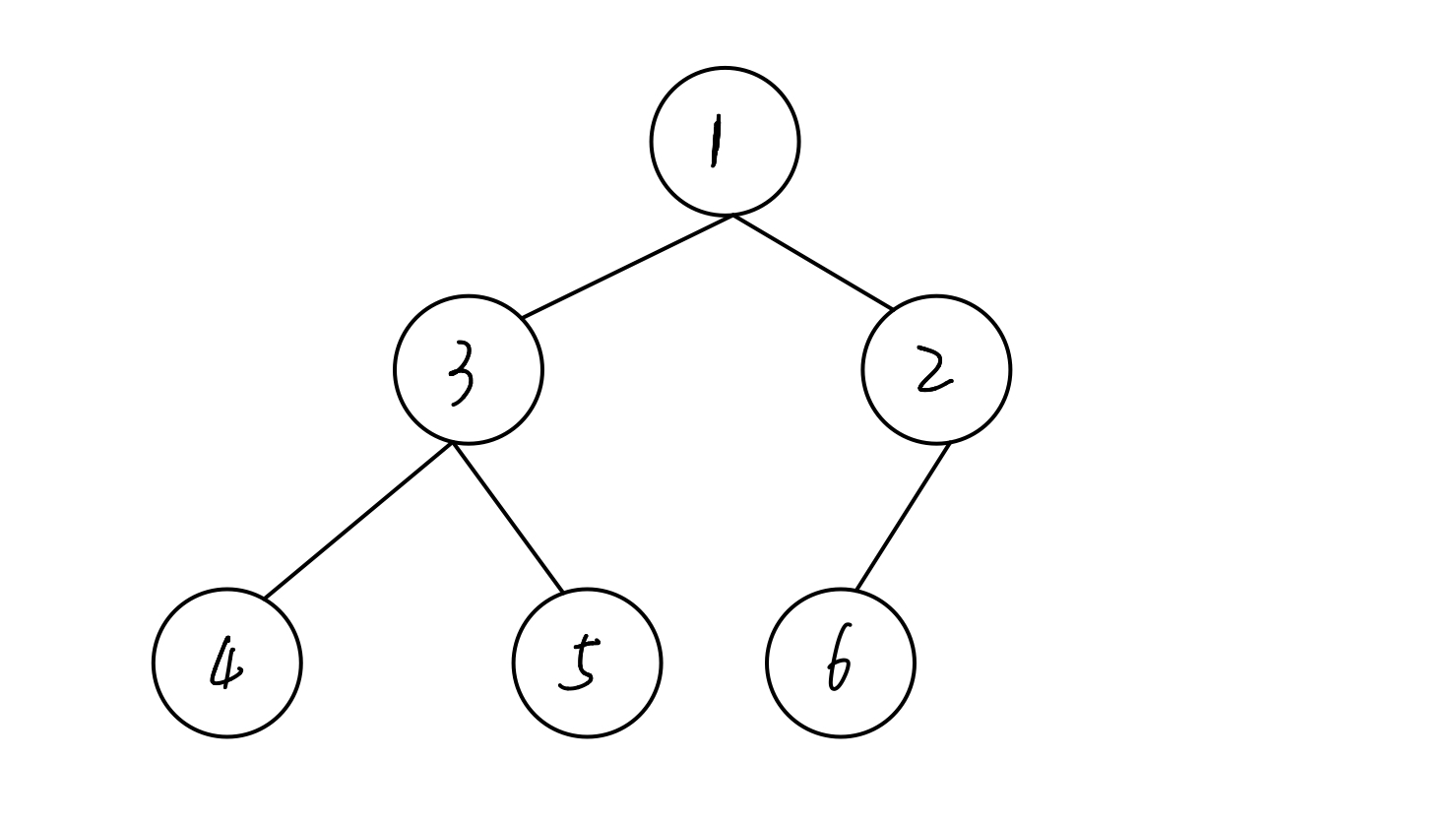
答案：是

解析：这是一个完全二叉树，并且所有节点都小于其孩子节点的值。

创建堆

创建 堆 指的是初始化一个堆实例。所有堆方法的前提必须是在堆实例上进行操作。换句话说，我们必须要首先创建一个 堆 实例，然后才能使用 堆 的常用方法。在创建 堆 的过程中，我们也可以同时进行 堆化 操作。堆化 就是将一组数据变成 堆 的过程。

时间复杂度：O(N)。

空间复杂度：O(N)。

// Java中的堆可以用优先队列(PriorityQueue)来表示
import java.util.Collections;
import java.util.PriorityQueue;
import java.util.Arrays;
// 创建一个空的最小堆
PriorityQueue minHeap = new PriorityQueue<>();
// 创建一个空的最大堆
PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());

// 创建带初始值的「堆」， 或者称为「堆化」操作，此时的「堆」为「最小堆」
PriorityQueue heapWithValues= new PriorityQueue<>(Arrays.asList(3,1,2));

扩展延伸：Python 最小堆转换城最大堆的逻辑

插入元素

插入操作指的是向 堆 中插入一个新元素。值的注意的是，新元素插入完毕后，堆 依旧需要维持它的特性。

时间复杂度：O(logN)。

空间复杂度：O(1)。

// 最小堆插入元素
minHeap.add(1);
// 最大堆插入元素
maxHeap.add(1);

获取堆顶元素

// 最小堆获取堆顶元素，即最小值
minHeap.peek();
// 最大堆获取堆顶元素，即最大值
maxHeap.peek();

删除堆顶元素

// 最小堆删除堆顶元素
minHeap.poll();
// 最大堆删除堆顶元素
maxheap.poll();

获取堆的长度

堆 的长度可以用来判断当前堆的大小，也可以用来判断当前堆是否还有元素。如果当前堆中没有元素，则 堆 的长度为 0。

时间复杂度：O(1)

空间复杂度：O(1)

// 最小堆的长度
minHeap.size();
// 最大堆的长度
maxHeap.size();
// 注意：Java中判断堆是否还有元素，除了检查堆的长度是否为0外，还可以使用isEmpty()方法。
// 如果堆中没有元素，则isEmpty()方法返回true。
// 如果堆中还有元素，则isEmpty()方法返回false。

时间复杂度和空间复杂度

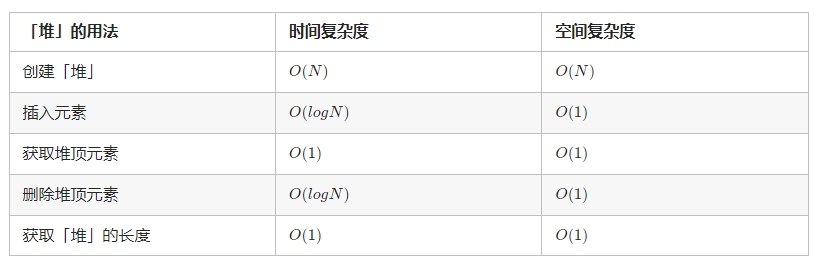
完整代码

// 最小堆完整代码
import java.util.PriorityQueue;
public class App {
    public static void main(String[] args) {
        // 创建一个最小堆实例
        PriorityQueue minHeap = new PriorityQueue<>();
        // 分别往最小堆中添加3，1，2
        minHeap.add(3);
        minHeap.add(1);
        minHeap.add(2);
        // 查看最小堆的所有元素，结果为：[1, 3, 2]
        System.out.println("minHeap: "+minHeap.toString());
        // 获取最小堆的堆顶元素
        int peekNum = minHeap.peek();
        // 结果为：1
        System.out.println("peek number: "+peekNum);
        // 删除最小堆的堆顶元素
        int pollNum = minHeap.poll();
        // 结果为：1
        System.out.println("poll number: "+pollNum);
        // 查看删除1后最小堆的堆顶元素，结果为：2
        System.out.println("peek number: "+minHeap.peek());
        // 查看新的最小堆的所有元素，结果为：[2,3]
        System.out.println("minHeap: "+minHeap.toString());
        // 查看最小堆的元素个数，也是最小堆的长度
        int heapSize = minHeap.size();
        // 结果为：2
        System.out.println("minHeap size: "+heapSize);
        // 判断最小堆是否还有元素
        boolean isEmpty = minHeap.isEmpty();
        // 结果为： false
        System.out.println("isEmpty: "+isEmpty);
    }
}

堆排序

理论：堆排序指的是利用堆的数据结构对一组无序元素进行排序。

最小堆 排序算法步骤如下：

1. 将所有元素堆化成一个 最小堆 ；
2. 取出并删除堆顶元素，并将该堆顶元素放置在存储有序元素的数据集 T 中；
3. 此时，堆 会调整成新的 最小堆；
4. 重复 3 和 4 步骤，直到 堆 中没有元素；
5. 此时得到一个新的数据集 T，其中的元素按照 从小到大 的顺序排列。

最大堆排序算法步骤如下：

1. 将所有元素堆化成一个 最大堆；
2. 取出并删除堆顶元素，并将该堆顶元素放置在存储有序元素的数据集 T 中；
3. 此时，堆 会调整成新的 最大堆；
4. 重复 3 和 4 步骤，直到 堆 中没有元素；
5. 此时得到一个新的数据集 T，其中的元素按照从大到小的顺序排列。

时间复杂度：O(NlogN)。
N是 堆 中的元素个数。

空间复杂度：O(N)。N是 堆 中的元素个数。

Top K 问题 – 解法 1

理论：利用「堆」的数据结构获取 Top K 大的元素或者 Top K 小的元素。

Top K 大元素：最大的 K 个元素；

Top K 小元素：最小的 K 个元素。

「Top K 大元素」解法步骤：

1. 创建一个「最大堆」；
2. 将所有元素都加到「最大堆」中；
3. 通过 「边删除边遍历」（大部分语言中为pop()或者poll()） 方法，将堆顶元素删除，并将它保存到结果集 T 中；
4. 重复 3 步骤 K 次，直到取出前 K 个最大的元素；

「Top K 小元素」解法步骤：

1. 创建一个「最小堆」；
2. 将所有元素都加到「最小堆」中；
3. 通过 「边删除边遍历」（大部分语言中为 pop() 或者 poll()） 方法，将堆顶元素删除，并将它保存到结果集 T 中；
4. 重复 3 步骤 K 次，直到取出前 K 个最小的元素；

时间复杂度：O(KlogN)

空间复杂度：O(N)

Top K 问题 – 解法 2

理论：利用「堆」的数据结构获取 Top K 大的元素或者 Top K 小的元素。

Top K 大元素：最大的 K 个元素；

Top K 小元素：最小的 K 个元素。

「Top K 大元素」解法步骤：

1. 创建一个大小为 K 的「最小堆」；
2. 依次将元素添加到「最小堆」中；
3. 当「最小堆」的元素个数达到 K 时，将当前元素与堆顶元素进行对比：

   如果当前元素小于堆顶元素，则放弃当前元素，继续进行下一个元素；

   如果当前元素大于堆顶元素，则删除堆顶元素，将当前元素加入到「最小堆」中。

4. 重复步骤 2 和步骤 3，直到所有元素遍历完毕。
5. 此时「最小堆」中的 K 个元素就是前 K 个最大的元素。

「Top K 小元素」解法步骤：

1. 创建一个大小为 K 的「最大堆」；
2. 依次将元素添加到「最大堆」中；
3. 当「最大堆」的元素个数达到 K 时，将当前元素与堆顶元素进行对比：
   1. 如果当前元素大堆顶元素，则放弃当前元素，继续进行下一个元素；
   2. 如果当前元素小于堆顶元素，则删除堆顶元素，将当前元素加入到「最小堆」中。
4. 重复步骤 2 和步骤 3，直到所有元素遍历完毕。
5. 此时「最大堆」中的 K 个元素就是前 K 个最小的元素。

时间复杂度：O(NlogK)

空间复杂度：O(K)

The Kth 问题 – 解法 1

理论：利用「堆」的数据结构获取 The Kth 大元素或者 The Kth 小元素。

The Kth 大元素：第 K 个大的元素；

The Kth 小元素：第 K 个小的元素。

「The Kth 大元素」解法步骤：

1. 创建一个「最大堆」；
2. 将所有元素都加到「最大堆」中；
3. 通过 「边删除边遍历」（大部分语言中为 pop() 或者 poll()） 方法，将堆顶元素删除；
4. 重复 3 步骤 K 次，直到获取到第 K 个最大的元素；

「The Kth 小元素」解法步骤：

1. 创建一个「最小堆」；
2. 将所有元素都加到「最小堆」中；
3. 通过 「边删除边遍历」（大部分语言中为 pop() 或者 poll()） 方法，将堆顶元素删除；
4. 重复 3 步骤 K 次，直到获取到第 K 个最小的元素；

时间复杂度：O(KlogN)

空间复杂度：O(N)

The Kth 问题 – 解法 2

理论： 利用「堆」的数据结构获取 The Kth 大元素或者 The Kth 小元素。

The Kth 大元素：第 K 个大的元素；

The Kth 小元素：第 K 个小的元素。

「The Kth 大元素」解法步骤：

1. 创建一个大小为 K 的「最小堆」；
2. 依次将元素添加到「最小堆」中；
3. 当「最小堆」的元素个数达到 K 时，将当前元素与堆顶元素进行对比：
   1. 如果当前元素小于堆顶元素，则放弃当前元素，继续进行下一个元素；
   2. 如果当前元素大于堆顶元素，则删除堆顶元素，将当前元素加入到「最小堆」中。
4. 重复步骤 2 和步骤 3，直到所有元素遍历完毕。
5. 此时「最小堆」中的堆顶元素就是第 K 个最大的元素。

「The Kth 小元素」解法步骤：

1. 创建一个大小为 K 的「最大堆」；
2. 依次将元素添加到「最大堆」中；
3. 当「最大堆」的元素个数达到 K 时，将当前元素与堆顶元素进行对比：
   1. 如果当前元素大于堆顶元素，则放弃当前元素，继续进行下一个元素；
   2. 如果当前元素小于堆顶元素，则删除堆顶元素，将当前元素加入到「最小堆」中。
4. 重复步骤 2 和步骤 3，直到所有元素遍历完毕。
5. 此时「最小堆」中的堆顶元素就是第 K 个最小的元素。

时间复杂度：O(NlogK)

空间复杂度：O(K)